二年级线段图怎么画-(线段图怎么画)
线段图是小学常见的且经常用到的一种帮助学生提高数学思维、分析解题技巧的一种方法,但也是学生学习的一个难点,没有正确画出线段图,反而会解决不了问题,扰乱学生的思维,加大解题难度。
那线段图是什么?
它是指通过一定意义的的线段、数字、箭头、符号所构成的平面图形,以表达数量关系为主要目的的图示。主要是以清晰的图形关系来表示来表达题目的的复杂的数量关系。

学生为什么要画线段图?
因为孩子看待事物,问题的时候,主要是通过事物的表象,就是具体事物的形象进行联想的。而不能有效的对事物的本质、关系、概念进行联想。也就是说孩子的思维处于具体化的思维模式,还没有向抽象化的思维模式转变。无法有效的判断题目中的数量关系,所以就需要借助“线段图”,来解决问题。
说个案例:有个老师,做了这么一个测试,同样的小学分数问题,让学生解答,没有用线段图,学生的正确率是47%,而用线段图的学生正确率是94%,可见线段图在小学数学中的重要性。学生应该正确掌握画线段图的方法。

怎么画线段图?
线段图的种类,一般分为三种:
1、单线式线段图:用一条线段来表示整体与部分的数量关系的线段图。
2、复式并列线段图:用两条或两条以上的线段来表示几个并列量的数量关系线段图。
3、变式线段图:在复式并列线段图的基础上进行移动、变形,来表示数量关系的线段图。
画线段图的常规步骤:
①画出标准量(找单位“1”)
②表示部分量或比较量
③标注所求问题
(画变式线段图,可根据具体问题灵活运用)
单式线段图
例:一袋食盐用去1/4,还剩600克,这袋食盐有多少克?
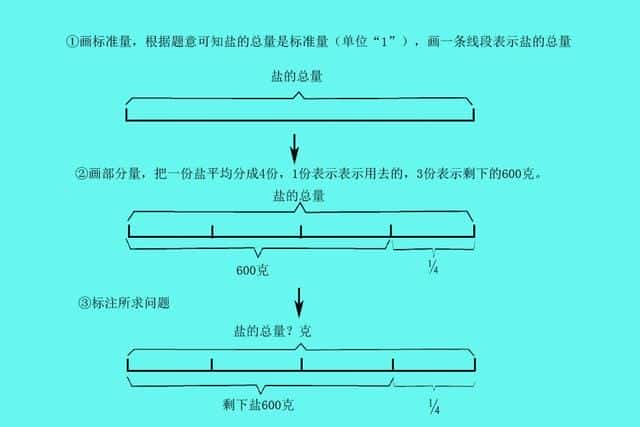
首先找标准量,通常在一个整体中,总数和部分数比较,把总数看做表现量(也就是单位“1”)
①从图上看,很容易看出数量关系,盐的总量平均分成四份,3份表示600克,一份就表示200克,有四份,所以盐的总量等于800克。
600÷3=200
200×4=800克
盐有800克。
②根据公式计算

比较量(部分数)÷对应分率=标准量(总数)
600÷3/4=800克
盐有800克
例:有一条绳子减去全长的三分之一,还剩3米,这条绳子有多长?
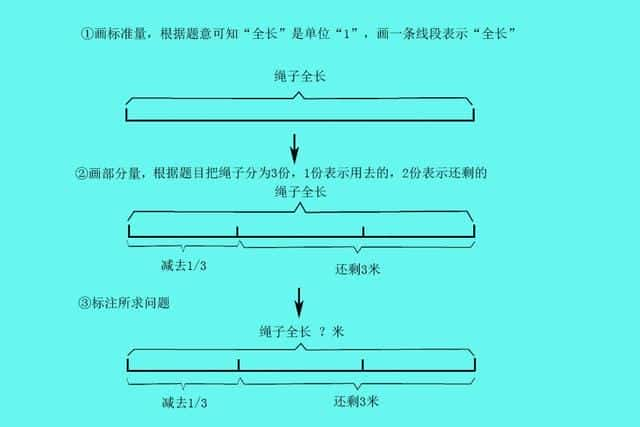
同一个整体中,把总数看做标准量。
①从图中来看,绳子全长平均分成3份,2份对应3米,一份就是1.5米,所以全长就是4.5米。
3÷2=1.5
1.5×3=4.5
绳子有4.5米长
②根据公式
比较量÷对应分率=标准量
3÷2/3=4.5米
绳子有4.5米长
例:有一桶水,第一次倒出40%,第二次比第一次少12千克,桶里还剩28千克,这桶水原来有多少千克?
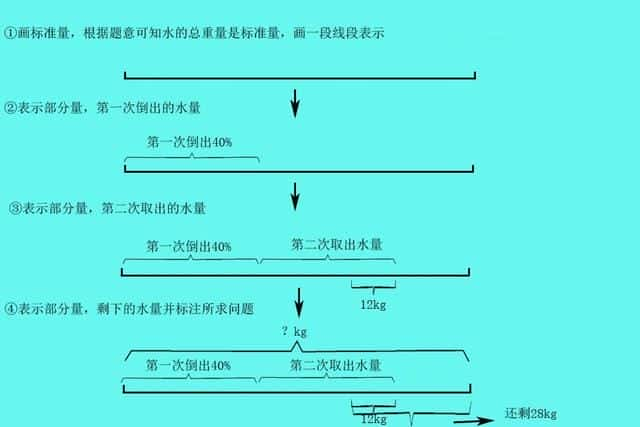
同一个整体中,把总数看做标准量。
①从图中看,第一次倒出40%,第二次和第一次相比少12千克,而少的这12千克是包含在剩余的28千克中的,剩余(28-16)千克,从线段图上看,这16千克对应的就是两次用了之后剩余的的(1-40%-40%),总量是单位“1”,对应的就是五份20%,是80千克
28-12=16
(1-40%-40%)÷20%=5
16×5=80
这桶水原来有80千克
②而水的总量就应该是线段图表示剩下的数量除以对应的分率。
根据公式
比较量÷对应分率=标准量
(28-12)=16
(1-40%-40%)=20%
16÷20%=80
这桶水原来有80千克
复式并列线段图
例:小明买一套衣服花了240元,买一套衣服比买一双运动鞋贵1/3,买一双运动鞋要多少钱?
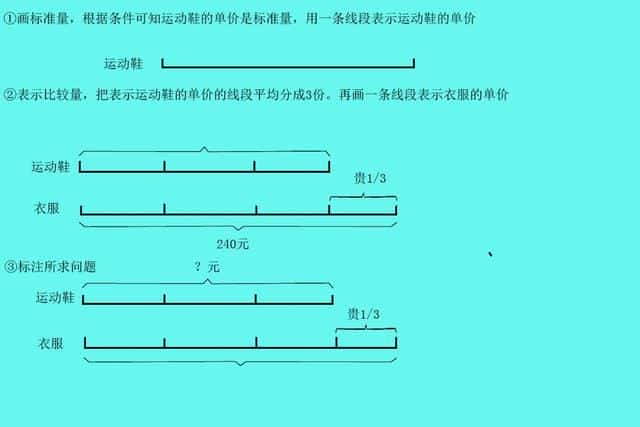
首先找标准量,不同数量相比较时,一般把后者看做标准量。
①从线段图上看,衣服的单价对应的是4份,运动鞋的单价对应的是3份
衣服对应的单价是240元,那么一份就是60元,
运动鞋的单价就是180元。
240÷4=60元
60×3=180元
运动鞋180元
②运动鞋的单价+1/3运动鞋的单价=衣服的单价
衣服的单价是240元,运动鞋的单价是标准量也就是单位“1”,对应分率是4/3。
根据公式
比较量÷对应分率=标准量
240÷4/3=180元
运动鞋要180元
例:一只海象的寿命是40年,海狮的寿命是海象的3/4,海豹的寿命是海狮的2/3,求海豹的寿命是多少年?
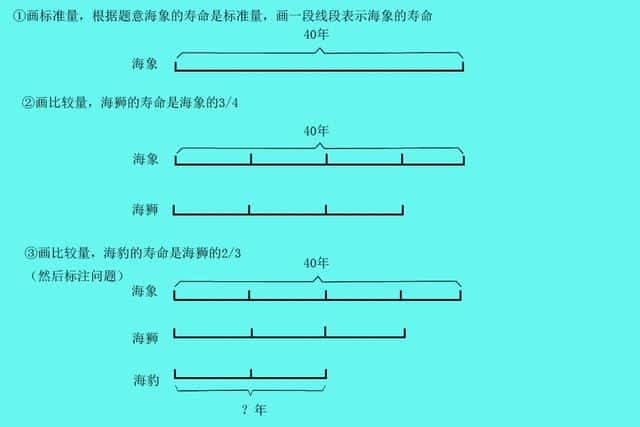
找标准量,不同数量相比较时,把后者看做标准量。
①从图形上看,海象总寿命对应的四份,海狮对应的是三份,海豹对应的是两份。算出海象对应的一份,带入相对应的动物中,就能得到
一份:40÷4=10
海狮:3×10=30
海豹:2×10=20
海豹寿命是20年。
②用公式计算就是
标准量×对应分率=比较量
海狮:40×3/4=30
海豹:40×2/4=20
海豹的寿命是20年
变式线段图
例:一批工件,第一次运走全部工件的1/3多20箱,第二次运走全部工件的1/4多30箱,这时货物还剩30箱。这批货物一共有多少箱?
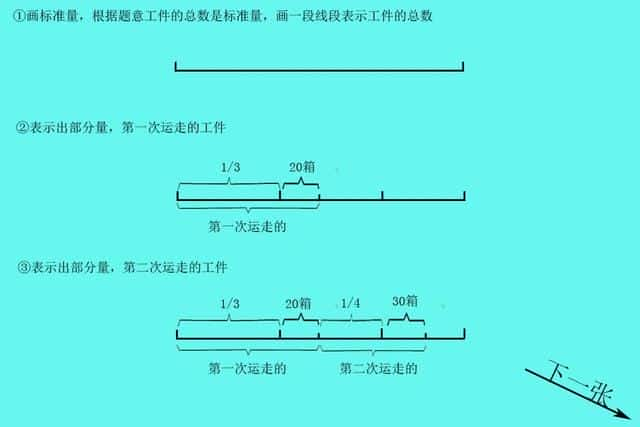
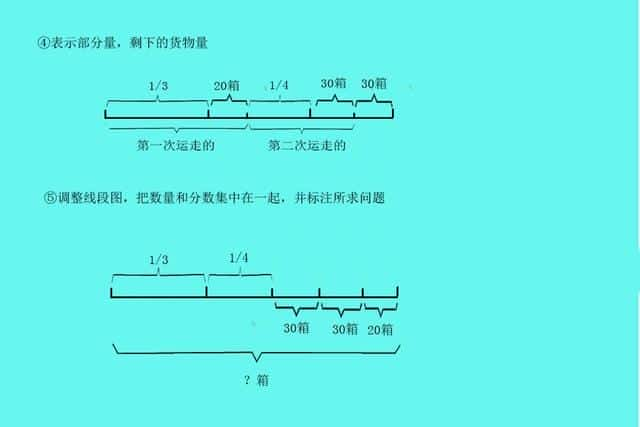
同一个整体中,把总数看做标准量。
观察上图发现,(20+30+30)对应货物总量的剩下的部分量。用(20+30+30)除以对应分率就可以求出货物总量。
根据公式
部分量÷对应分率=标准量
20+30+30=80
80÷(1-1/4-1/3)=192
一共192箱货
例:一辆卡车和一辆轿车同时从A、B两地相对开出,两车在途中距A地60千米处第一次相遇。然后两车继续前进,卡车到达B地、轿车到达A地后立即返回,两车又在途中距B地30千米处相遇。A、B两地相距多少千米?
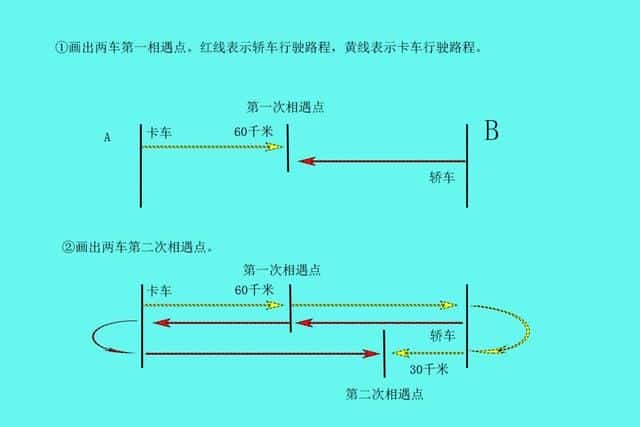
观察图形,卡车和轿车在第一次相遇的时候(也就是两车共行驶第一个全程),卡车行驶了60千米
两车第二次相遇时,两车共行驶了三个全程,则卡车共行驶了60×3=180(千米)。
由图可知,卡车共行驶了一个全程还多30千米,所以用180-30所得的差就是A、B两地之间的路程。
60×3-30=150(千米)
A、B两地相距150千米。
总结
注意分析题目,找准标准量,才能画出准确的线段图。学好线段图,可以帮助学生快速解答问题,提高数学分析能力、思维能力。
欢迎下方留言,交流不同经验。