散度定理—向量微积分的基本定理,深入理解其背后的思想和直觉
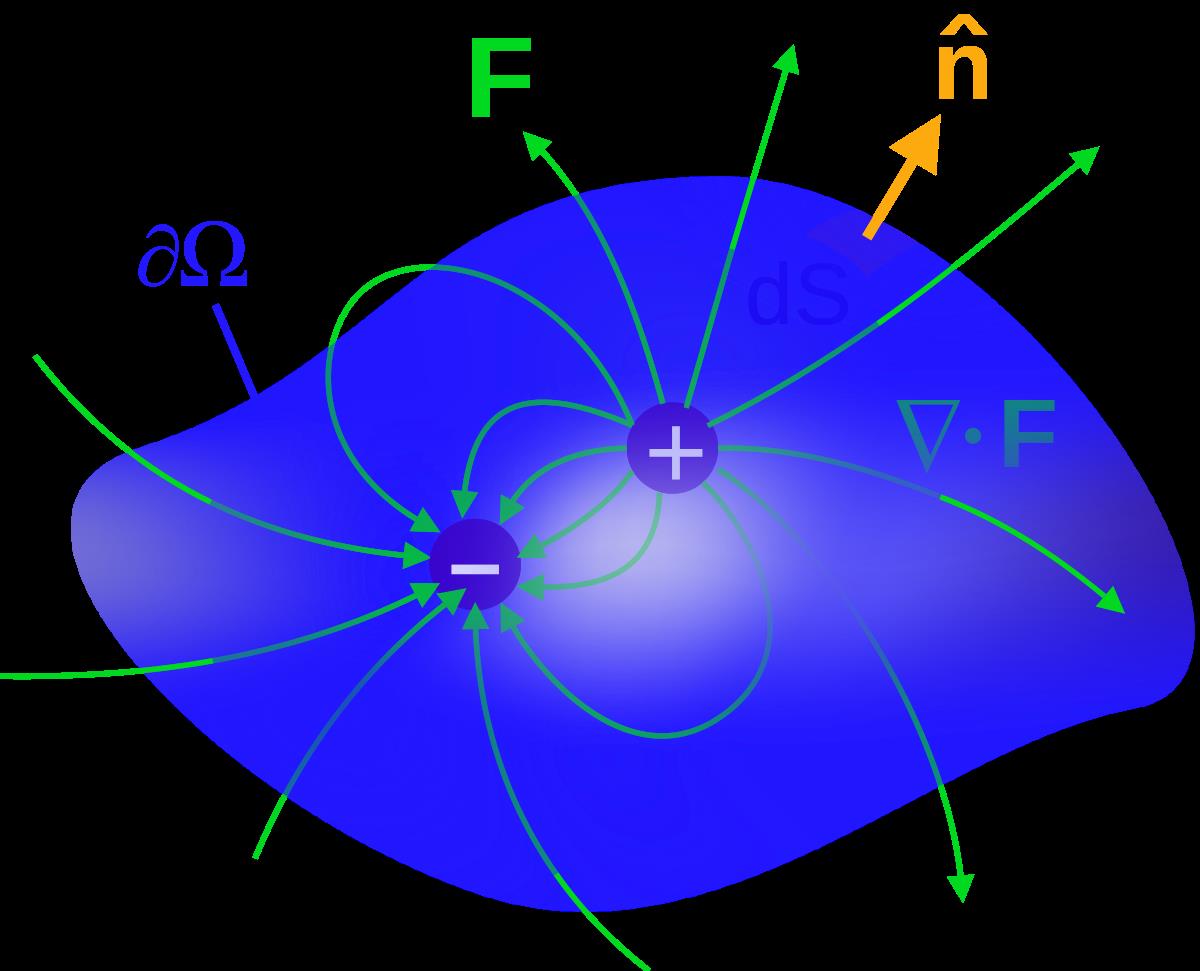
在数学和物理领域,我们常常需要处理空间中的矢量场,这些矢量场可能描述物理现象如电场或磁场,或者可能仅仅是抽象的数学对象。而在这其中,一个关键的数学工具就是散度定理((divergence integral theorem)),也被称为高斯定理或高斯-奥斯特罗格拉茨基定理。它是向量微积分中的基础定理之一,提供了关于矢量场在某个区域内部和通过区域边界的行为之间的深刻联系。该定理不仅在理论研究中有着重要作用,也对于计算机图形学、电磁学、流体动力学等实际应用领域有着巨大价值。在本文中,我们将深入探讨散度定理的内涵,并试图通过直观和严谨的方式来解释这个强大的数学工具。
以下是散度定理的样子:
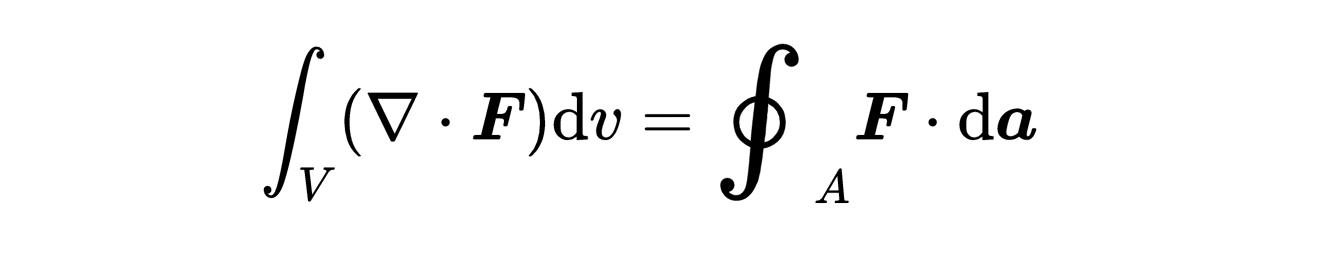
首先,让我们看一下等式的右边,
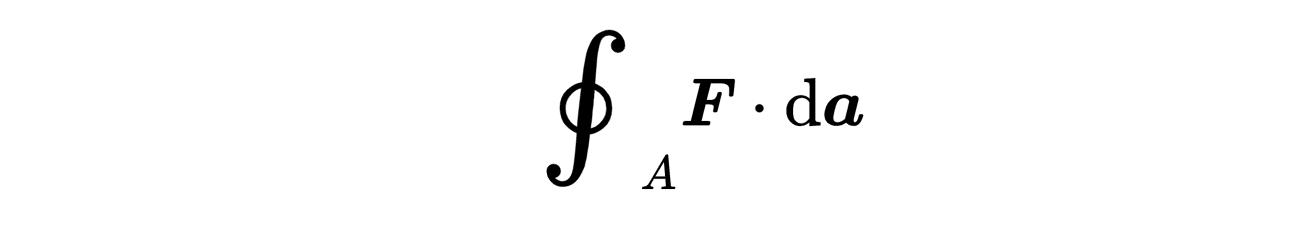
这里的A代表一个封闭任何体积的表面,例如立方体、球体或者你能想到的任何三维物体的表面。

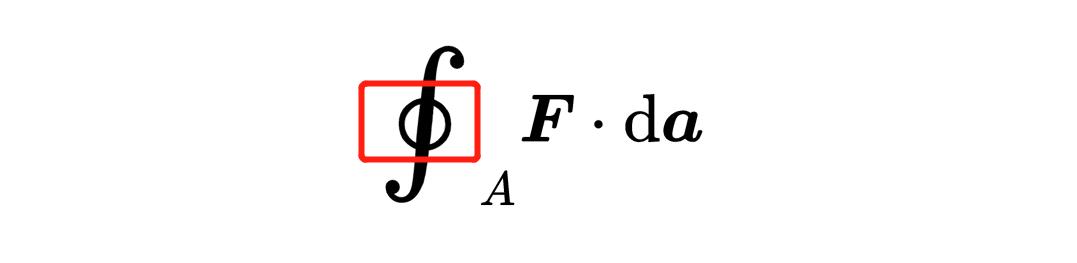
在积分符号上的小圆圈表明这个表面必须满足一个条件:表面必须是封闭的,也就是说,它不能包含任何的孔洞,以便在数学上保证这个条件。因此,表面a就是一个封闭的表面。
这里的F是一个矢量场,可以表示电场
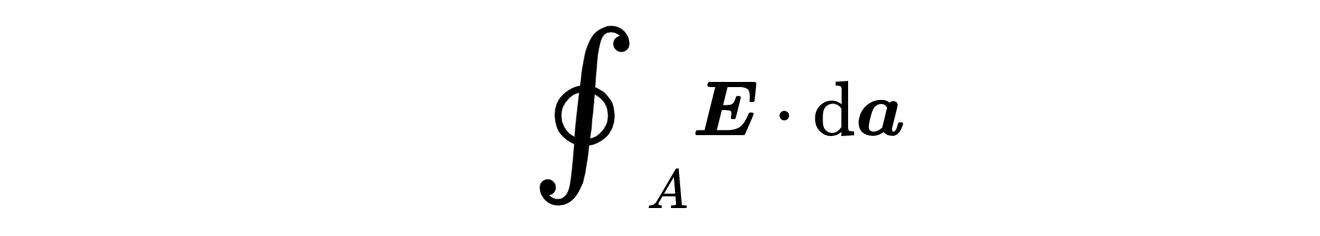
或磁场,
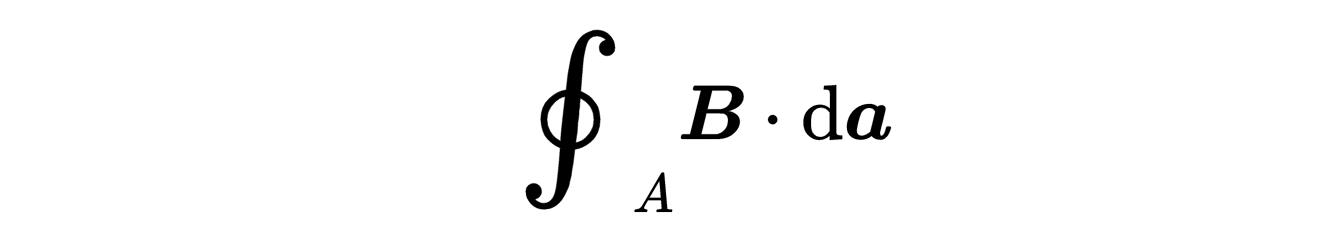
当我们在考虑麦克斯韦方程的时候,它是一个有三个组成部分的矢量,
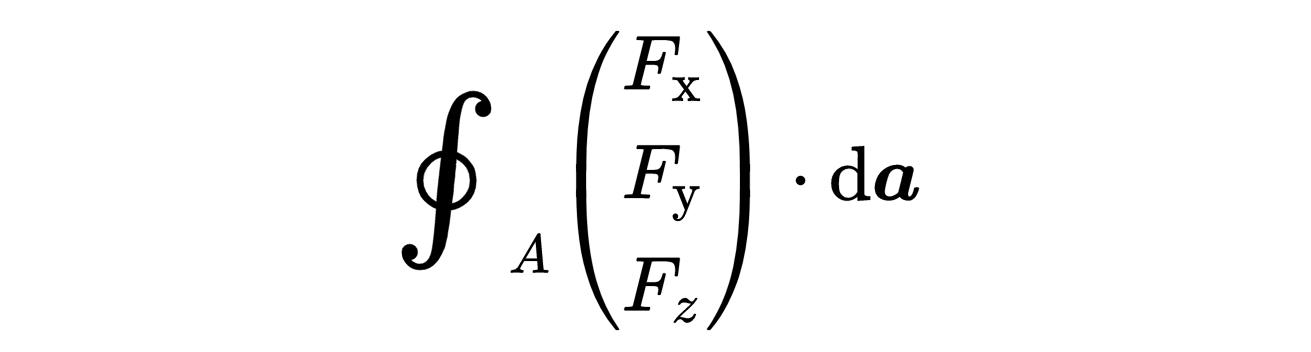
da 是无穷小的表面元素,就是所考虑的表面A的无穷小表面元素。

你可能已经注意到,da 元素中的a是加粗的,所以它是一个有大小和方向的矢量。 da元素垂直于表面,并且定义为从表面指向外部。
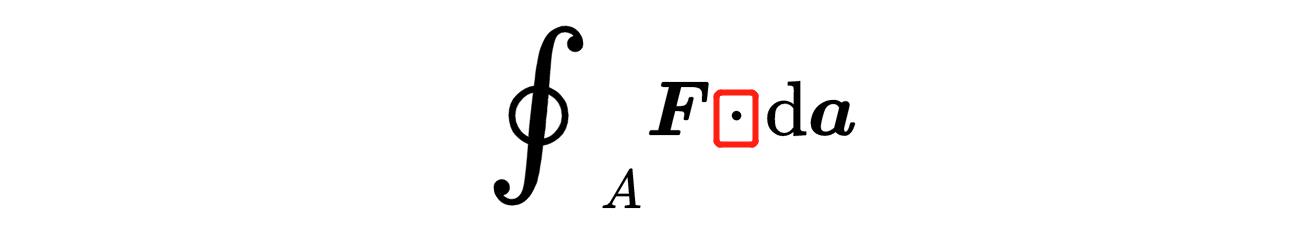
在矢量场和da元素之间的点代表所谓的标量积。标量积是一种乘两个矢量的方法,所以在这里,矢量场和da 元素之间的标量积是形成的。标量积的定义如下:
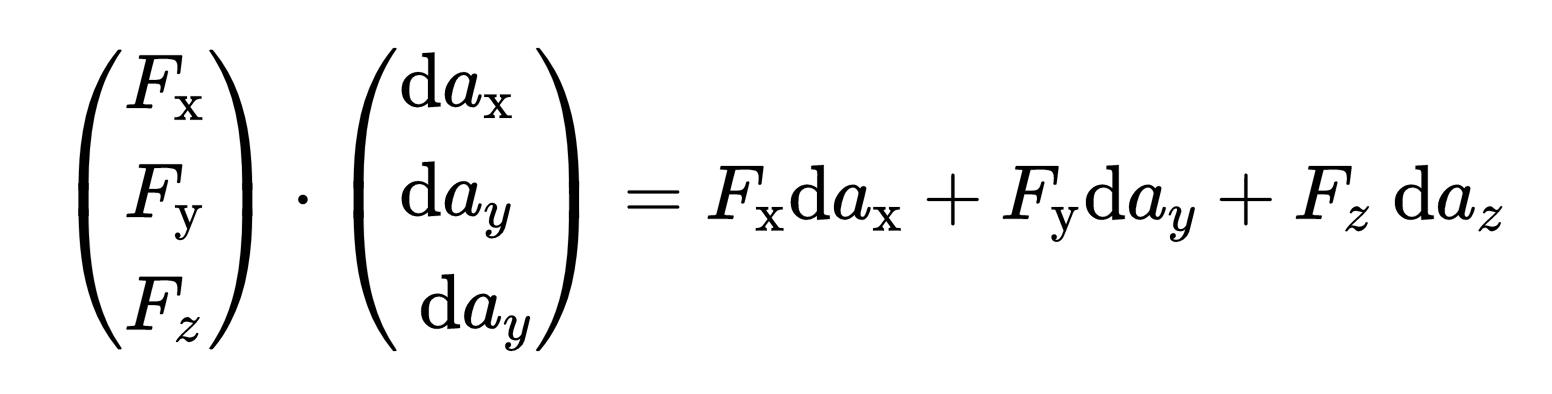
从定义中可以看出,两个矢量的第一,第二和第三组成部分是相乘然后相加的。标量积的结果不再是一个矢量,而是一个普通的数字。
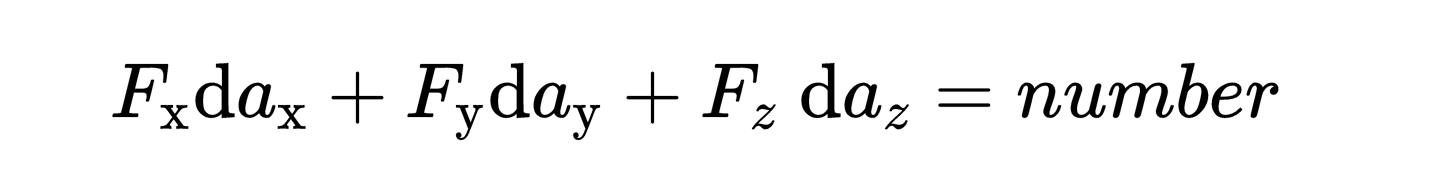
为了理解这个数字的含义,你首先要知道任何矢量都可以写成两个其他矢量的和,
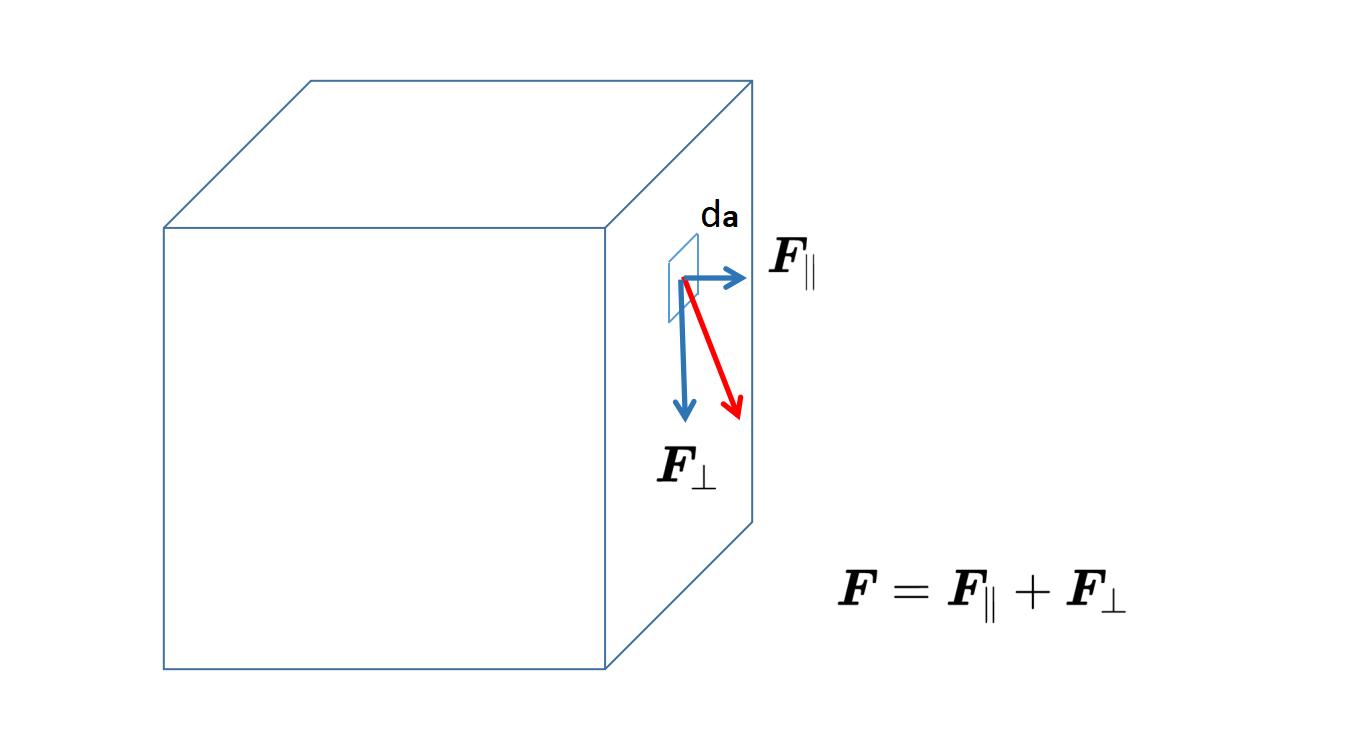
其中一个矢量平行于da元素,我们称之为F平行,另一个矢量垂直于da 元素,我们称之为F垂直。另一个数学事实是,两个垂直矢量的标量积总是等于零,这就意味着,
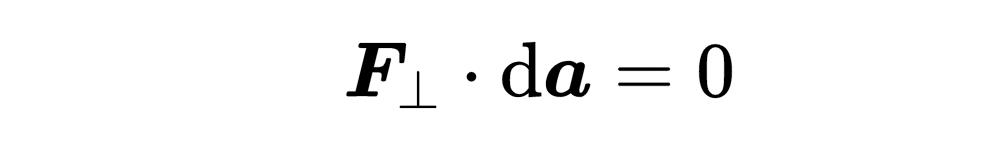
然而,F平行和da 元素之间的标量积通常不是零,
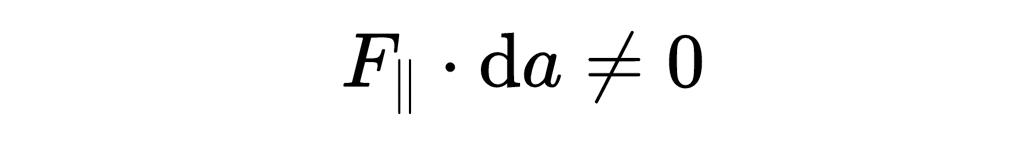
所以现在你可以看到等式右边的标量积是怎么计算的,
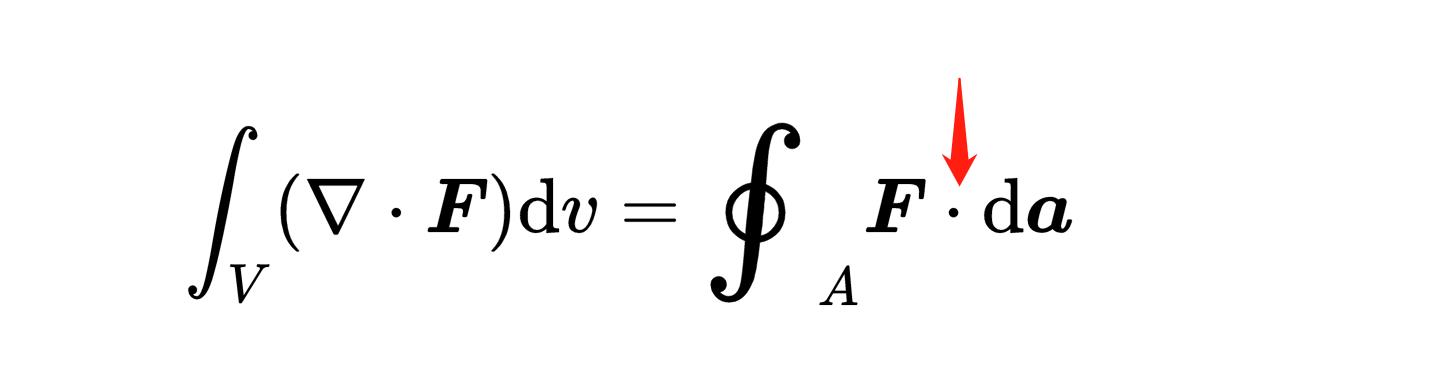
它只选择了矢量场中和da 元素平行的部分,剩下的在垂直方向上的矢量场部分被标量积消除。
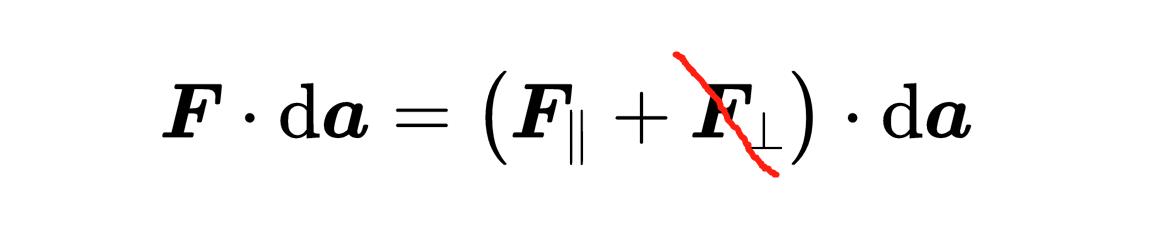
接下来,对于被考虑的表面A的所有位置,都会累加标量积,这就是积分的任务,
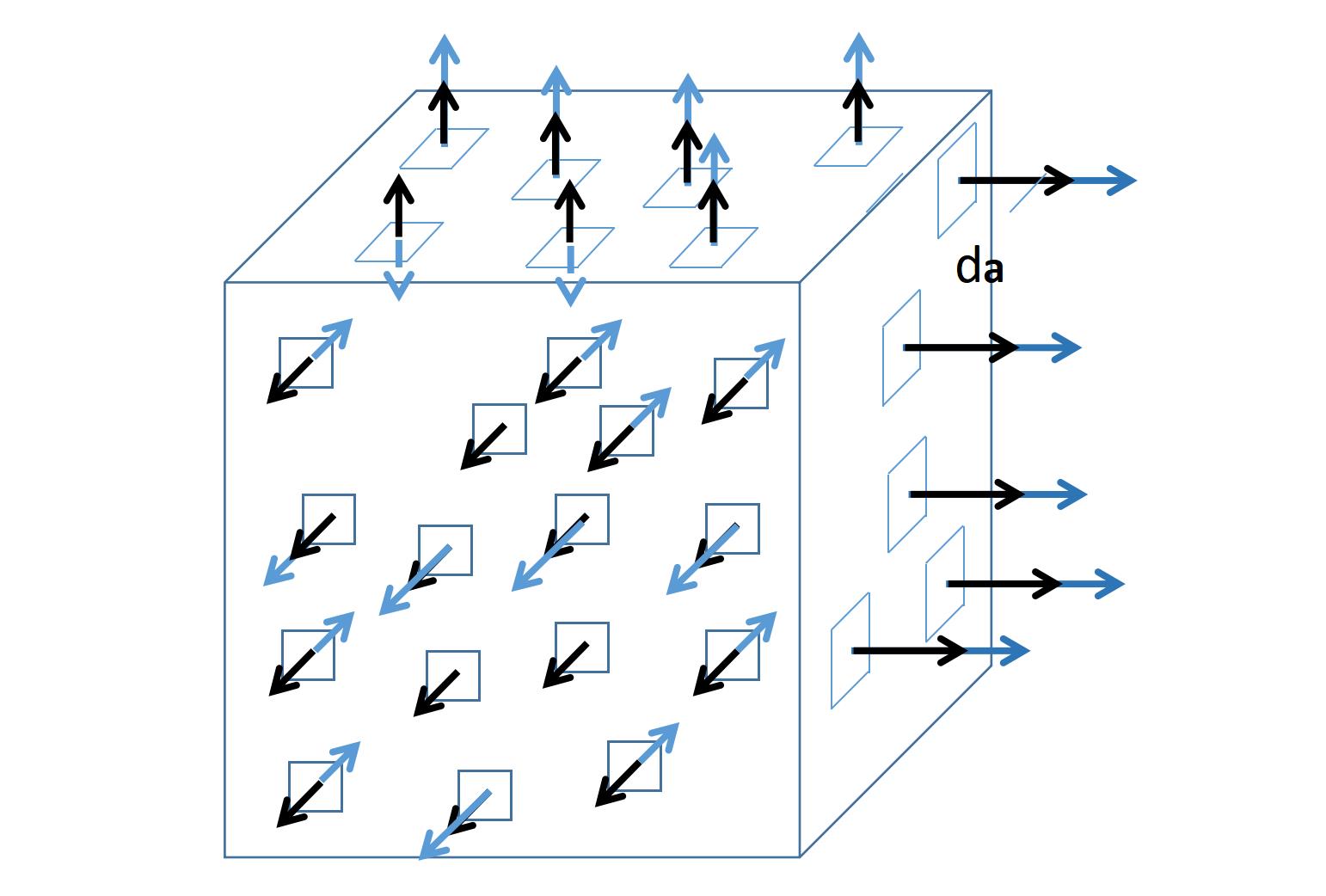
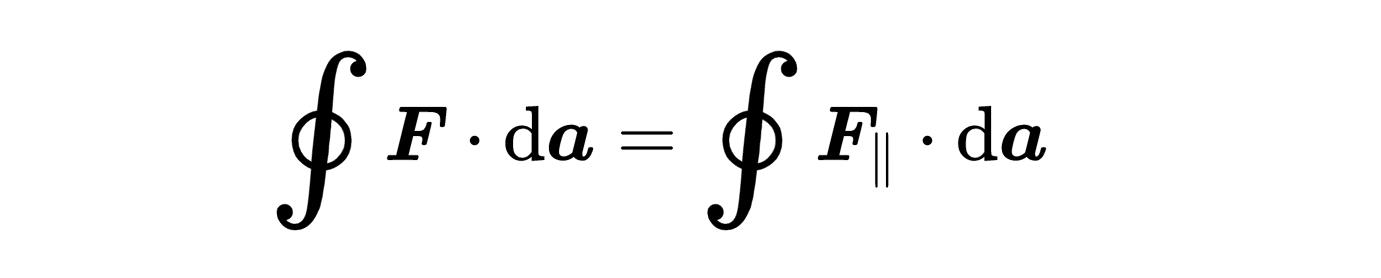
因此,散度定理的右侧会求和所有流入或流出表面A的矢量场F的分量。这种对表面的小片段进行求和的积分被称为表面积分(surface integral)。如果积分函数是一个矢量场,这个表面积分被称为矢量场F通过表面A的流量ϕ。
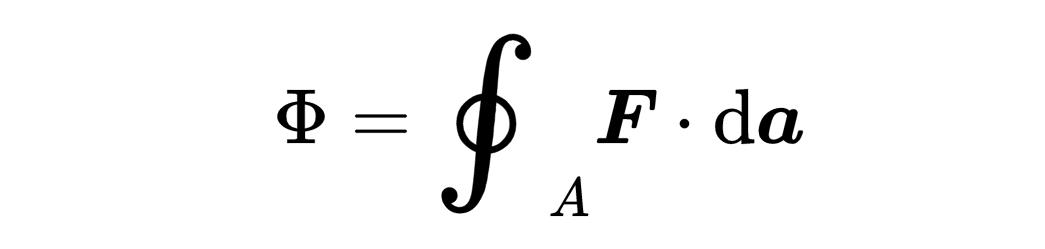
这个描述基于这个表面积分的意义,它度量了多少的矢量场F流出或流入被考虑的表面A。
如果这个表面积分的矢量场F是电场E,那么这个表面积分就被称为通过表面A的电通量。如果矢量场F是磁场B,那么这个表面积分就被称为通过表面A的磁通量。
现在让我们看看定理的左侧,
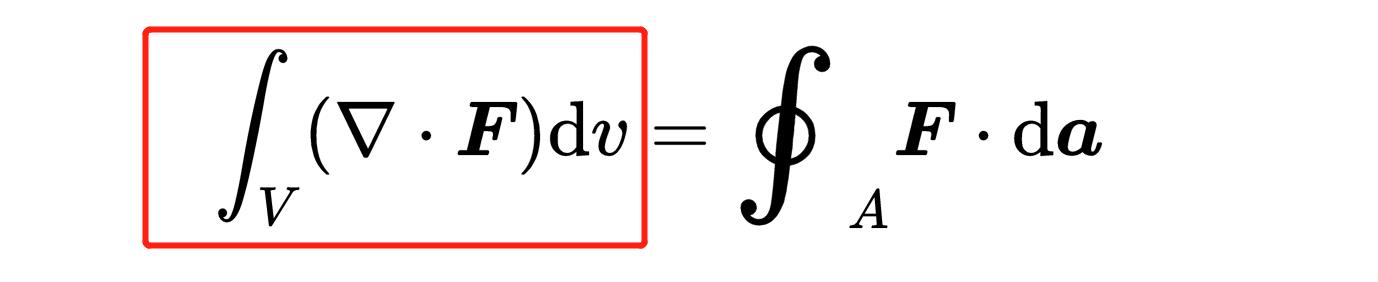
V是一个体积,它是由表面A封闭的体积。dv是一个无穷小的体积元素,换句话说,它是被考虑的体积V的无穷小的体积片段。
上下三角符号被称为nabla算子,它有三个组成部分,就像矢量一样,
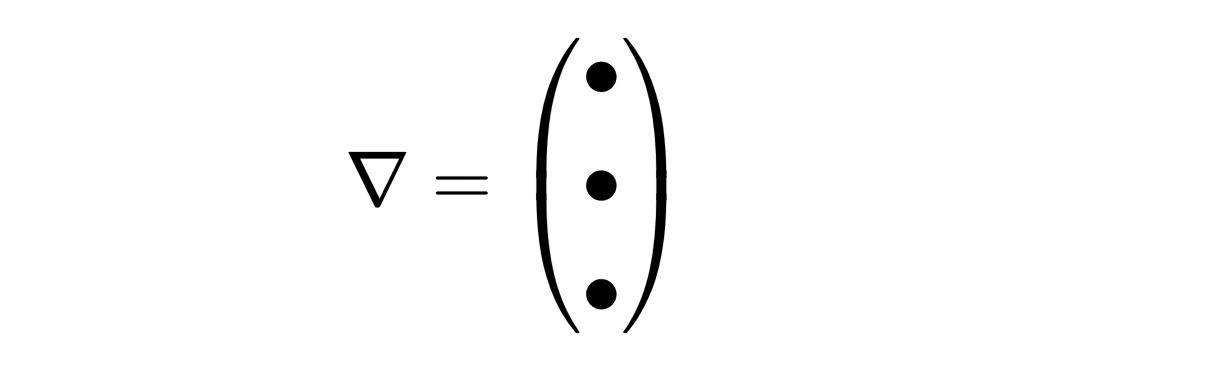
然而,它的组成部分不是数字,而是导数,对应于空间坐标。第一个组成部分是关于x的导数,第二个组成部分是关于y的导数,第三个组成部分是关于z的导数。
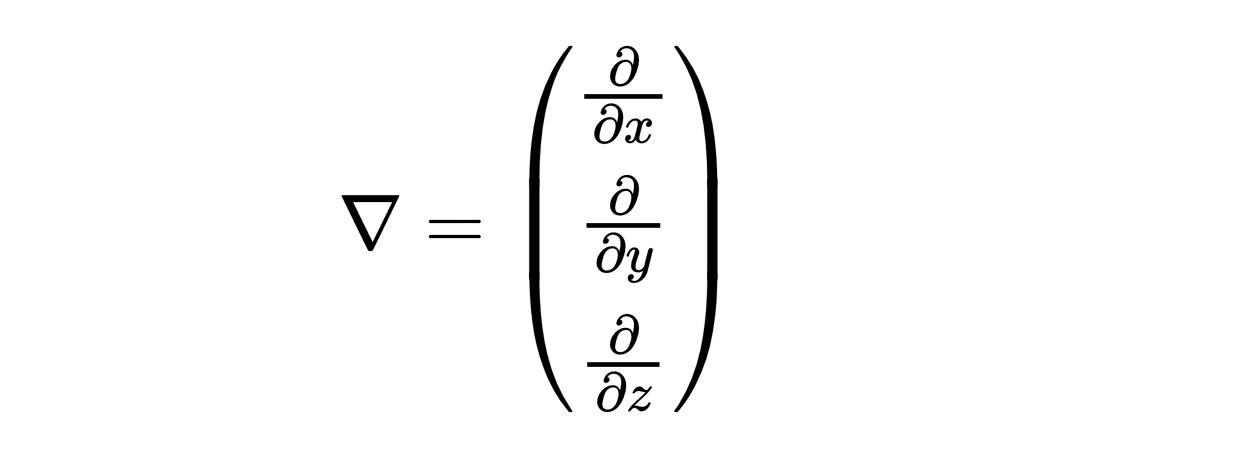
像nabla算子这样的算子只在应用到一个场时起作用,
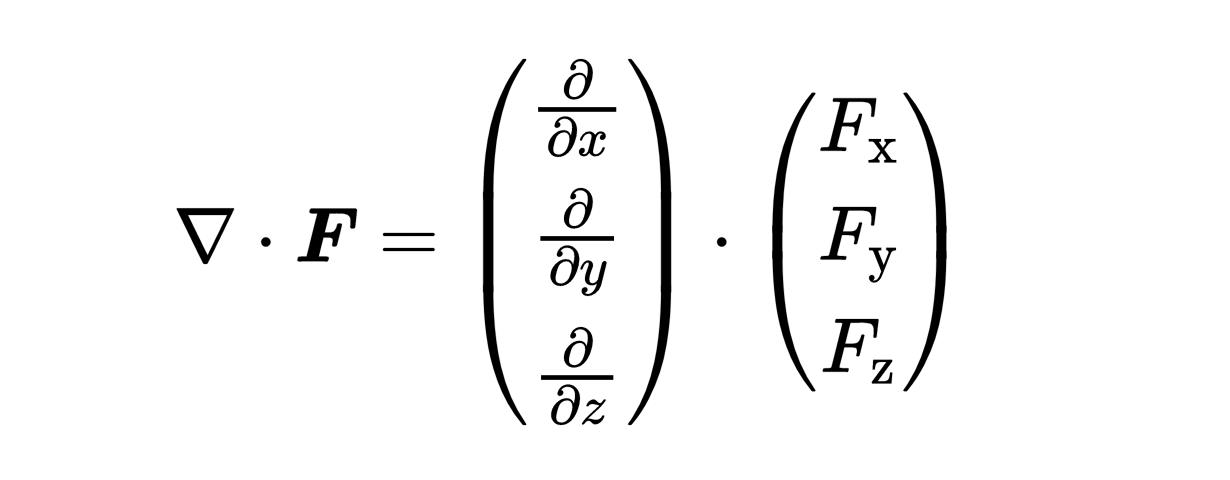
nabla算子应用到矢量场,通过在nabla算子和矢量场之间取标量积。你可以看到,这是矢量场对空间坐标x, y, z的导数的和,
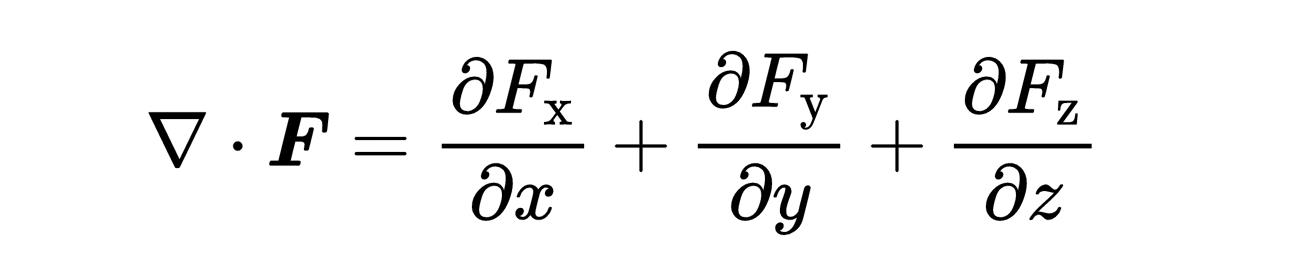
这样一个nabla算子和矢量场F之间的标量积被称为矢量场F的散度(Divergence of F)。在位置x, y, z的结果不再是一个矢量,而是一个标量,它可以是正的,负的,或者是零。
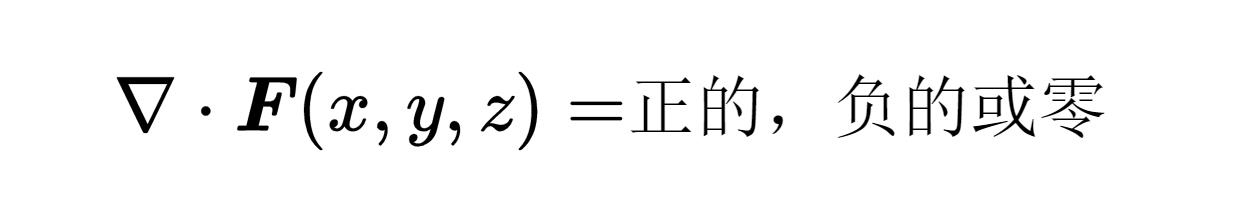
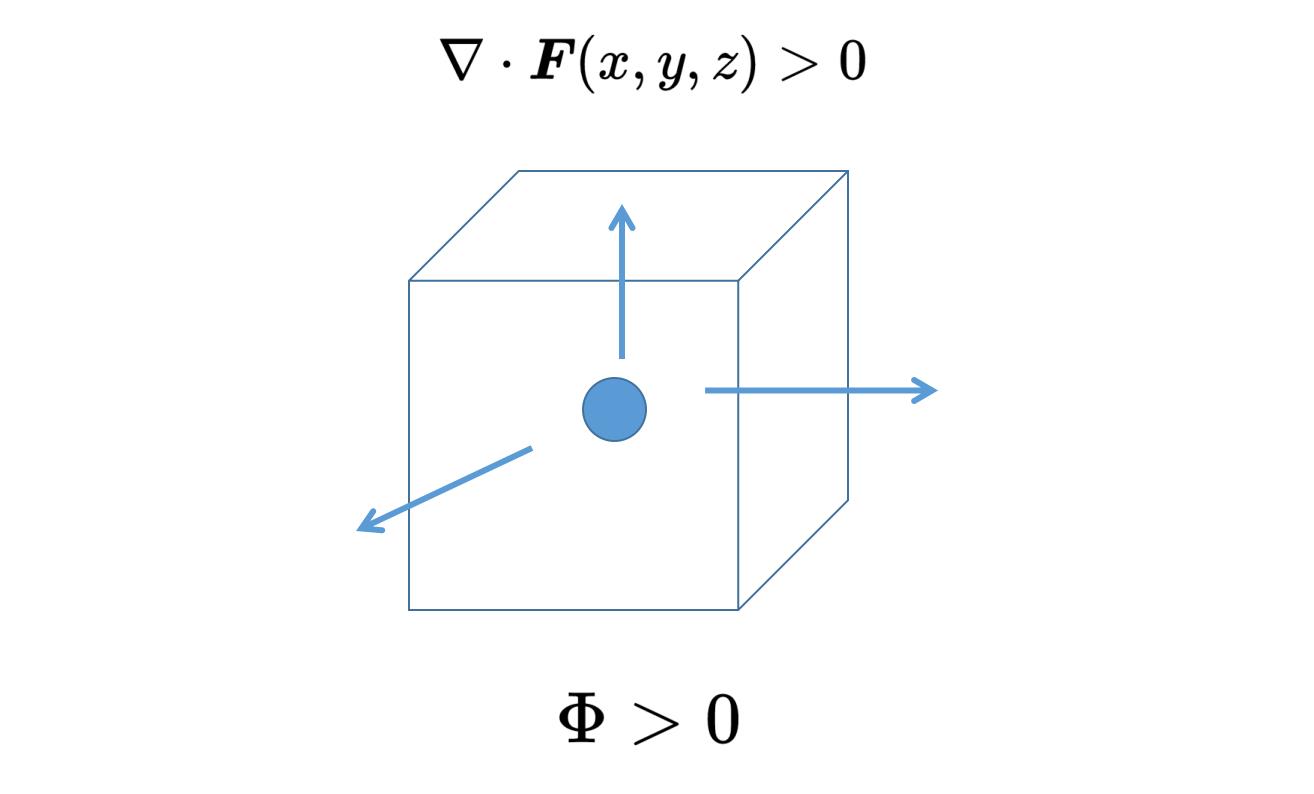
如果在位置x, y, z的散度是正的,那么在这个位置(下图正方体中的圆点)有一个矢量场F的源。如果这个位置被表面包围,那么通过表面的通量也是正的,矢量场可以说是从表面流出。
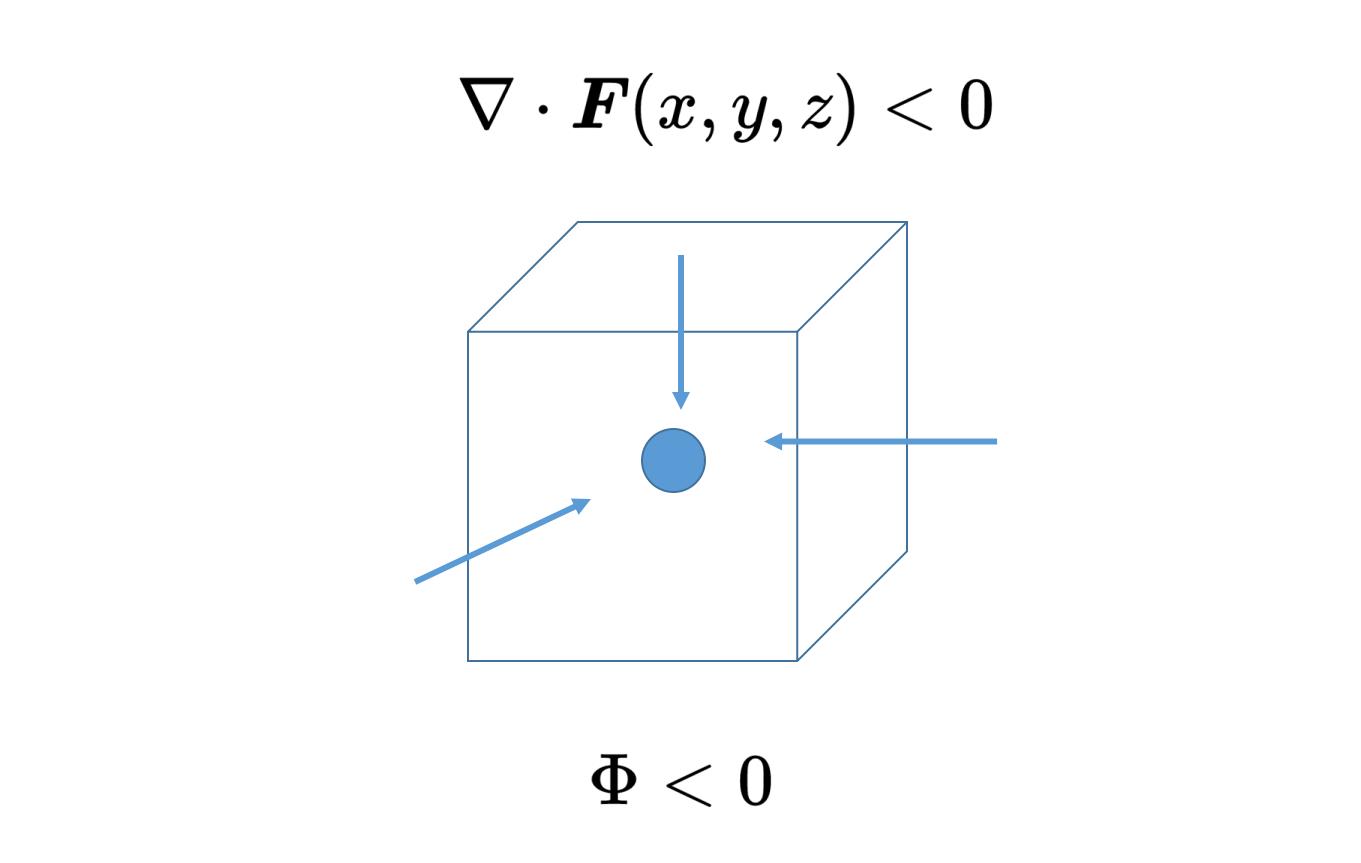
如果在位置x, y, z的散度是负的,那么在这个位置(下图正方体中的圆点)有一个矢量场F的汇,如果这个位置被表面包围,那么通过表面的通量也是负的,矢量场流入表面。
如果在位置x, y, z的散度消失,那么这个位置既不是矢量场的汇也不是源。矢量场不会流出或流入,或者说流入的和流出的数量相等,所以这两个量抵消了。

接下来,利用积分在体积内的每一个位置求和散度,即矢量场的源和汇。这种对体积小片段求和的积分被称为体积积分。
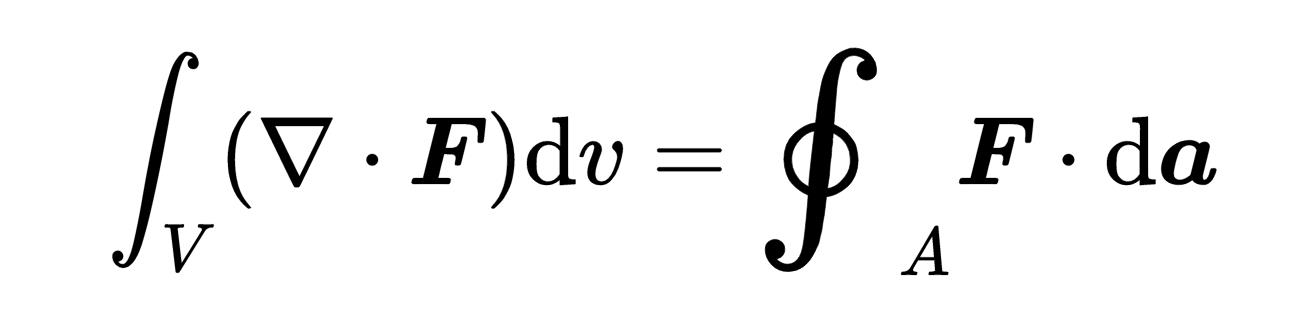
那么让我们总结一下散度定理:在左边是矢量场在体积内的源和汇的总和,而在右边是矢量场通过那个体积的表面的总通量,这两边应该是相等的。散度定理因此表明,在一个体积内的矢量场的源和汇的总和,就是矢量场通过那个体积的表面的通量。
















